通过模拟社会网络验证友谊悖论

为什么你的朋友总看起来比你更受欢迎?

友谊悖论简介

友谊悖论是一种社会现象, 指大多数人认为, 自己的朋友比自己拥有更多的朋友. 该社会现象由社会学家斯科特·L·菲尔德 (Scott L. Feld) 于1991年首次观察到。

这一现象可以直观上解释为抽样偏差的一种表现形式, 即一个人如果本身拥有较多朋友, 那么这个人更有可能同时也是自己的朋友; 而一个人如果本身朋友就很少, 那么这个人和自己成为朋友的可能也会较小.

这样的社会现象也常常出现在其他场合, 如学术圈内, 大多数人认为, 自己的合作者比自己发表了更多的论文; 再如社交媒体上, 大多数人认为, 自己关注的人比自己拥有更多的粉丝.

理论分析

我们用图论的方法来对这一现象进行分析. 将社交网络用一张无向图 $G=(V,E)$ 来表示, 其中 $V$ 为图中的节点集, 表示社交网络中的人; $E$ 为图中的边集, 表示社交网络中的人际关系. 两个人 $i$ 与 $j$ 是朋友当且仅当 $i,j\in V$ 且 $(i,j)\in E$, 即在图 $G$ 中节点 $i$ 和节点 $j$ 之间存在边. 定义 $d(v)$ 为节点的度, 即与它相连的节点个数, 对应着表示一个人的朋友个数.

一张社会网络图如下所示:

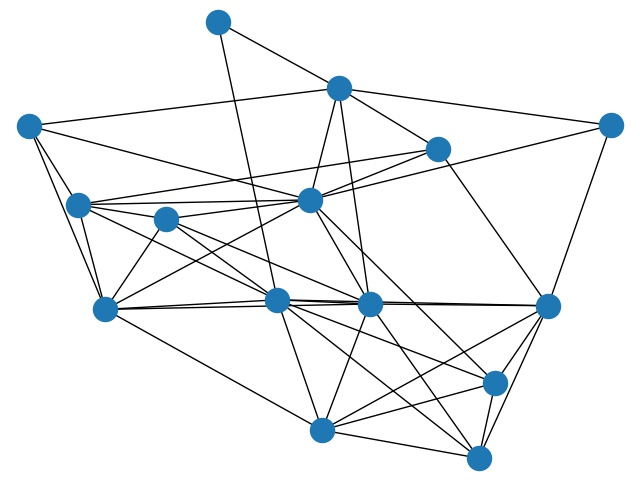
如果说一个人满足了"友谊悖论", 当且仅当在图 $G$ 中, 他所对应的顶点 $v$ 满足

$$d(v)<\frac{\sum_{u\in V} d(u)\mathbf{1}_E((u,v))}{d(v)}$$

这里 $\mathbf{1}_A(x)$ 为指示函数:

$$\mathbf{1}_A(x)=\left\{ \begin{array}{**lr**} 1& x\in A\\ 0 & x\notin A\end{array} \right.$$

那么对于社交网络中的所有人, 其平均朋友个数即为图 $G$ 所有点的平均度数, 应当为

$$\overline n=\frac{\sum_{v\in V}d(v)}{|V|} = 2\frac{|V|}{|E|}$$

下面随机选择一个人 $v$, 然后估算他朋友的平均朋友数量.

这等价于选择一个是别人朋友的人, 然后估算他的朋友数量.

这等价于随机选择图的中的一条边 (表示具有朋友关系的一对人), 再随机选择该边的一个端点, 计算该端点的度数.

每个端点被选到的概率为 $\displaystyle \frac{d(v)}{2|E|}$. 这是由于共有 $|E|$ 条边, 而与 $v$ 相连的边共有 $d(v)$ 条, 选到每条边的概率为 $\displaystyle \frac{d(v)}{|E|}$, 而每条边都有两个端点, 因此最终每个端点被选到的概率为 $\displaystyle \frac{d(v)}{2|E|}$.

因此, 随机选择一个是别人朋友的人, 其朋友的数量的期望为:

$$\overline m = \sum_{v\in V}(\frac{d(v)}{2|E|})d(v)=\frac{\sum_{v\in V}d(v)^2}{2|E|}$$

这里 $\sum_{v\in V}d(v)^2 = |V|(\mu^2+\sigma^2)$, 其中 $\mu$ 是图中所有点度的均值, 有 $\mu = \displaystyle 2\frac{|V|}{|E|}$, $\sigma^2$ 是方差. 因此, 有 $\overline m = \displaystyle \frac{\mu^2 + \sigma^2}{\mu}$. 若方差 $\sigma^2 > 0$, 则一定有 $\overline m > \overline n$.

这意味着: 只要图的方差大于0, 那么有朋友的节点的平均度, 严格大于整张图的平均度.

社会网络模拟

在本节中, 我们通过撰写代码随机生成符合社会网络特征的图, 计算该图的所有节点中, 满足友谊悖论的占比.

这里我们使用了两种网络模型. 第一种是初始规则度数 $r$, 随机删除占比 $p$ 的边, 再随机添加占比 $p$ 的边. 我们称之为调整型网络. 第二种是直接让每个人随机选择一部分人成为自己的朋友. 我们称之为纯随机型网络.

我们使用 C++ 完成网络构造与友谊悖论的验证过程, 用 python 绘制直观的社交网络图.

调整型网络

网络模型

在该模型中, 社会网络的生成共分为三步.

• 生成 $n$ 个节点.
• 按指定的规律, 让每个节点和一部分节点连上边 (即每个人和一部分人成为朋友). 第 $i$ 个节点和第 $i+1,i+2,\cdots, i+r$个节点连边, 其中加法都在模 $n$ 的意义下进行.
• 在总共 $n\cdot r$ 条边随机选择占比为 $p$ 的边删除, 并将每条删掉的边, 随机选则新的边替代. 最终总边数仍为 $n\cdot r$.

这样的社交网络可以设想为这样的社会场景: 初始状态下每个人有一部分自己的朋友, 且大家的朋友分布有一定的规律性, 非常均匀. 而在网络随着时间演化的过程中, 人们随机结交新的朋友, 与过去的部分朋友逐渐断开联系, 这使得网络逐渐趋于不均匀.

该网络的两个主要函数如下:

for (int i = 0; i < MAX_N; ++i)
    for (int j = 1; j <= INI_N; ++j)
    {
        m[i][(i + j)%MAX_N] = 1;
        m[(i + j)%MAX_N][i] = 1;
    }
// 按设定的规律添加边

void changeEdge()
{
	int total = MAX_N * INI_N * CHANGE_R;
	for (int i = 0; i < total; ++i)
	{
		while (1)
		{	int changeI = rand() % MAX_N;
			int changeJ = rand() % MAX_N;
			if (m[changeI][changeJ])
			{
				cutEdge(changeI, changeJ); break;
			}
		}
		while (1)
		{
			int changeI = rand() % MAX_N;
			int changeJ = rand() % MAX_N;
			if (!m[changeI][changeJ])
			{
				addEdge(changeI, changeJ); break;
			}
		}
	}
}
// 随机删除旧边并添加新边

下面的两张图展示了调整前与调整后的网络. 为了方便绘图, 我们将节点数设置较少. 这里 $(n,p,r)=(15,4,0.35)$.

调整前

调整后

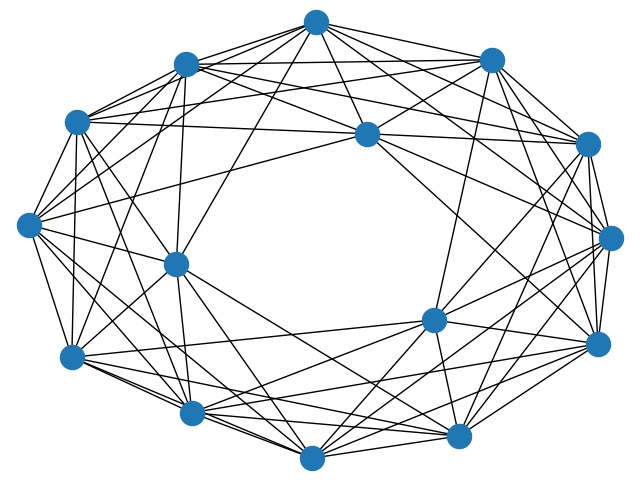
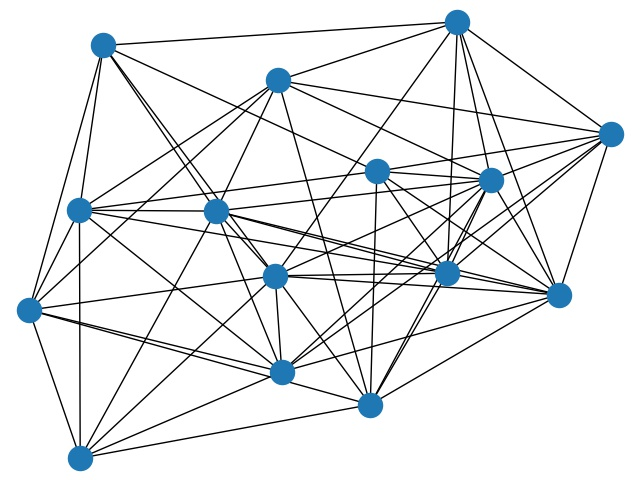
可以看出, 调整前网络整体非常均匀, 每个节点的度数都相等, 且关系特征明显; 调整后则不均匀度显著增大.

参数设置

该网络中共有三个参数: 节点数量 (总人数) $n$, 每个节点的初始度数 (每个人的初始朋友数量) $d = 2r$, 调整边占比 $p$.

注意这里 $d$ 和 $r$ 的区别. 每个节点"主动"与 $r$ 个节点连边, 又会"被动"与 $r$ 个节点连边, 因此每个节点的度数实际为 $2r$.

我们分别探究这三个参数 $(n,r,p)$ 对友谊悖论现象的影响. 使用控制变量法进行实验, 默认情况下, $n=100, r = 10, p = 0.2$. 在此基础上, $n$ 从 $50$ 变化到 $500$, 每次增加 $50$; $r$ 从 $3$ 增加到 $30$, 每次增加 $3$; $p$ 从 $0.1$ 增加到 $1.0$, 每次增加 $0.1$.

因变量为满足"友谊悖论"的节点占总节点数的比例, 表示为:

$$R = \frac{\sum_{v\in V}\left[d(v)<\frac{\sum_{u\in V} d(u)\mathbf{1}_E((u,v))}{d(v)}\right]}{|V|}$$

显然, 由 $R$ 的定义, 有 $0\leq R \leq 1$.

实验结果

对于上一节所说的三种控制变量方法, 我们依次开展实验, 探究 $r$ 随各个参数的变化.

总人数 $n$ 的实验

当 $r$ 与 $p$ 分别固定为 $10$ 与 $0.2$, 总人数 $n$ 从 $50$ 变化到 $500$, 每次增加 $50$ 时, $R$ 的变化如下图所示.

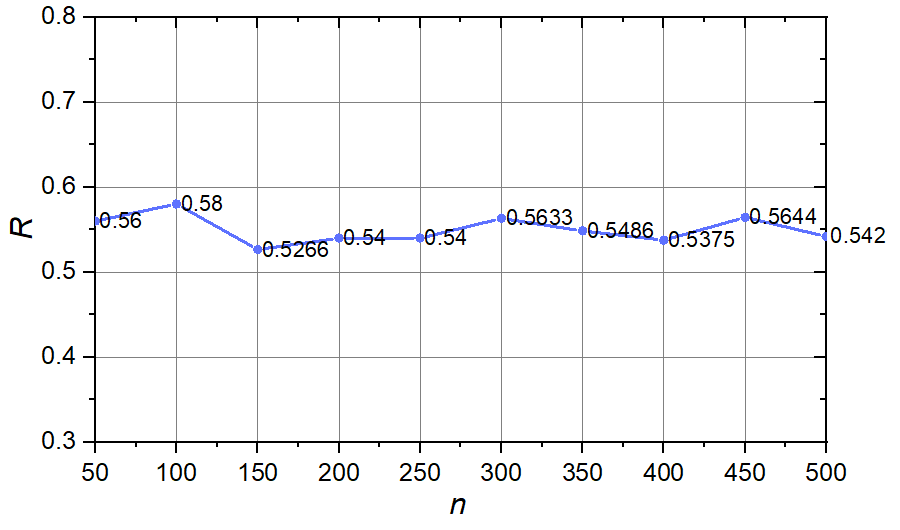
可以看到, 满足"友谊悖论"的人数占比整体上较稳定, 在 $[0.5, 0.6]$ 区间内, 且始终多于一半.

初始朋友数 $r$ 的实验

当 $n$ 与 $p$ 分别固定为 $100$ 与 $0.2$, 初始朋友数 $r$ 从 $3$ 增加到 $30$, 每次增加 $3$ 时, $R$ 的变化如下图所示.

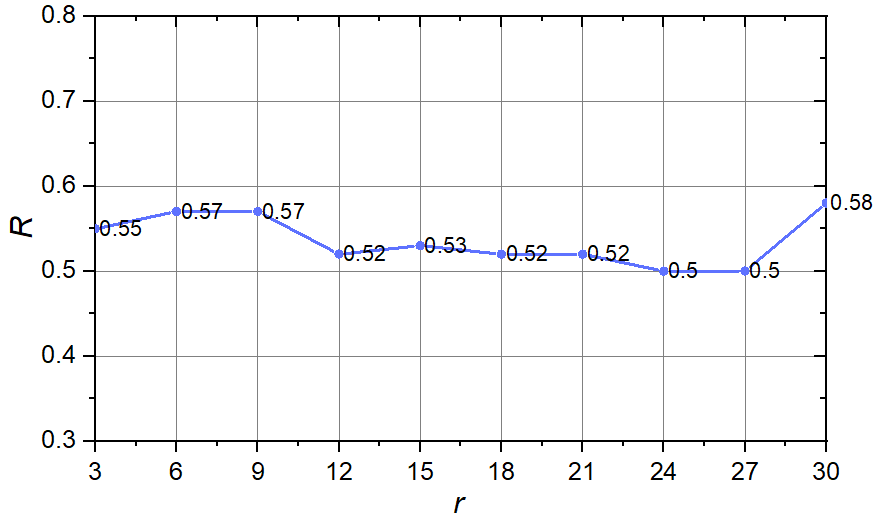
实验结果与上面类似, 可以看到, 满足"友谊悖论"的人数占比整体上较稳定, 在 $[0.5, 0.6]$ 区间内, 且始终不少于一半.

调整占比 $p$ 的实验

当 $n$ 与 $r$ 分别固定为 $100$ 与 $10$, 调整占比 $p$ 从 $0.1$ 增加到 $1$, 每次增加 $0.1$ 时, $R$ 的变化如下图所示.

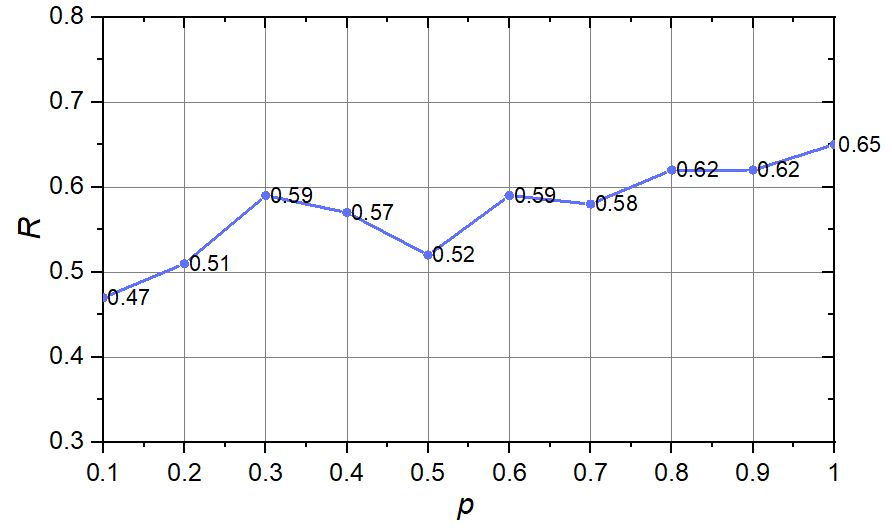
可以看到, 满足"友谊悖论"的人数占比呈现出递增趋势, 从最开始的不高于 $0.5$, 最终上升到 $0.65$. 这是因为随着调整的占比增大, 图的随机性越来越强.

随机型网络

网络模型

在该模型中, 社会网络的生成共分为两步.

• 生成 $n$ 个节点.
• 每个节点和随机选择 $r$ 个节点 ( $r$ 是固定的), 并与之连上边 (即每个人和随机和一定数量的人成为朋友).

这样的社交网络可以设想为这样的社会场景: 初始状态下所有人互不认识, 每个人随机地选择和一些人成为朋友. 注意这样的交友活动是一方发出与另一方接受, 且我们假设只要发出交友请求, 就一定会被接受. 这使得每个人发出一次请求, 就可以获得一个朋友关系. 每个人发出的请求数量是固定的, 即每个人都可以主动交固定数量的朋友.

注意, 朋友关系的形成有可能为一方主动一方接受, 也有可能为两方都主动都接受, 即 $i$ 向 $j$ 发出了朋友请求, $j$ 也向 $i$ 发出了朋友请求. 这种情况是被允许的.

直觉与经验告诉我们, 这样的社交网络中, 所有人的朋友数量应当是符合正态分布的: 即必定有少部分人"受欢迎", 最终的朋友数量很多; 而也有少部分人"被冷落", 最终的朋友数量很少; 但大多数人的朋友数量不多不少, 接近平均水平. 这个模型与现实更为接近. 下面对该现象进行数学分析.

现在任选一个人 $i$, 估计他的朋友数量. 由于总人数为 $n$, 他主动发出的朋友请求数为 $r$, 那么他的基础朋友数量都为 $r$. 现在考虑被动朋友数量.

对于任意一个人 $j(j\neq i)$, $j$ 主动向 $i$ 发出朋友请求的概率为$\displaystyle \frac{r}{n-1}$. 除去 $i$ 已经主动交友的 $r$ 个人外, 他还有可能收获的"被动朋友"还有 $n-r-1$ 个. 那么 $i$ 多收获 $x$ 个朋友的概率应当为:

$$p(x) =C_{n-r-1}^x \left(\frac{r}{n-1}\right)^x \left(1-\frac{r}{n-1}\right)^{n-1-x}$$

这实际上是一个二项分布. 当 $n$ 足够大时, 利用中心极限定理, 易知二项分布良好近似于正态分布.

下面是一个 $n=300, r=3$ 的例子. 横坐标为拥有的朋友数量, 纵坐标为拥有该数量朋友的人数. 可以看到拥有朋友数量的均值为 $2\cdot r$, 对应的人数也最多. 下图就是一个满足正态分布的例子.

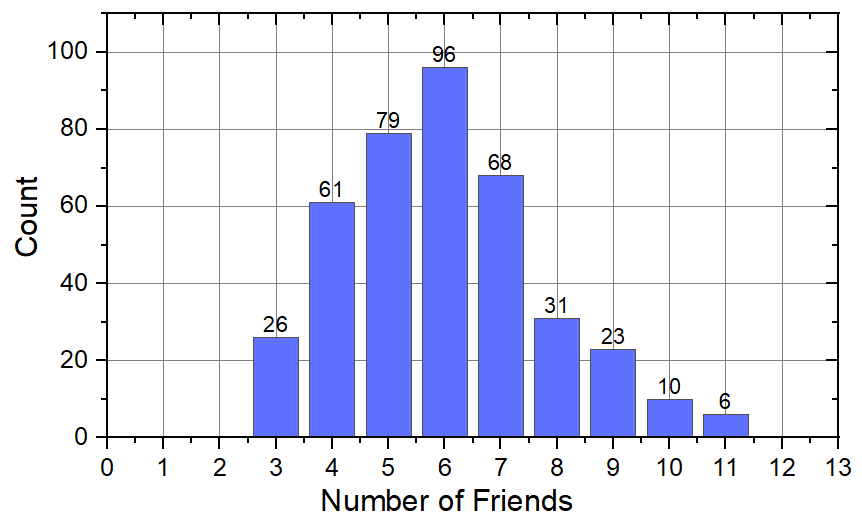
该网络的主要函数如下:

void iniEdge()
{
	for (int i = 0; i < MAX_N; ++i)
	{
		for (int j = 0; j < INI_N; ++j)
		{
			int resultJ = rand() % MAX_N;
			if (resultJ == i)continue;
			addEdge(i, resultJ);
		}
	}
}

参数设置

该网络中共有两个参数: 节点数量 (总人数) $n$, 每个节点的初始度数 (每个人的初始朋友数量) $d = 2r$.

注意这里 $d$ 和 $r$ 的区别. 每个节点"主动"与 $r$ 个节点连边, 又会"被动"与 $r$ 个节点连边, 因此每个节点的度数实际为 $2r$.

我们分别探究这两个参数 $(n,r)$ 对友谊悖论现象的影响. 使用控制变量法进行实验, 默认情况下, $n=100, r = 10$. 在此基础上, $n$ 从 $50$ 变化到 $500$, 每次增加 $50$; $r$ 从 $3$ 增加到 $30$, 每次增加 $3$.

类似上面, 因变量为满足"友谊悖论"的节点占总节点数的比例, 表示为:

$$R = \frac{\sum_{v\in V}\left[d(v)<\frac{\sum_{u\in V} d(u)\mathbf{1}_E((u,v))}{d(v)}\right]}{|V|}$$

显然, 由 $R$ 的定义, 有 $0\leq R \leq 1$.

实验结果

对于上一节所说的两种控制变量方法, 我们依次开展实验, 探究 $r$ 随各个参数的变化.

总人数 $n$ 的实验

当 $r$ 固定为 $10$ , 总人数 $n$ 从 $50$ 变化到 $500$, 每次增加 $50$ 时, $R$ 的变化如下图所示.

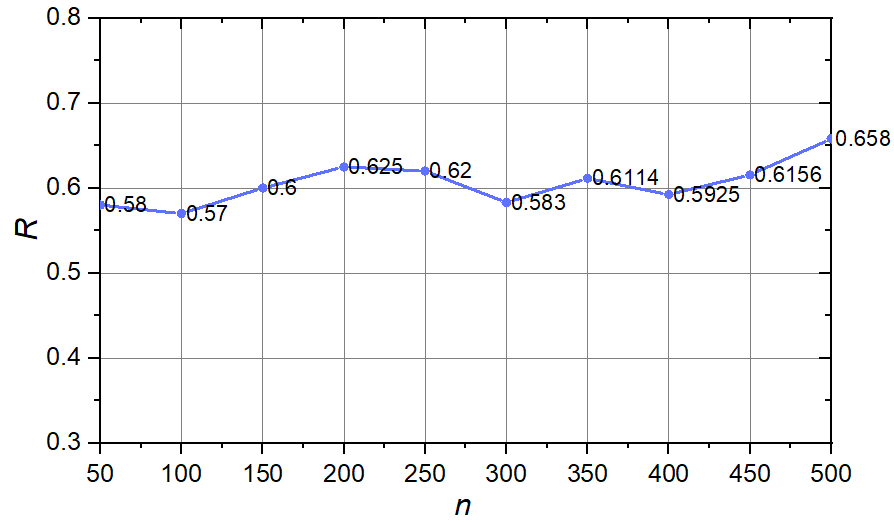
可以看到, 满足"友谊悖论"的人数占比整体上较稳定, 在 $[0.5, 0.7]$ 区间内, 且始终多于一半.

初始朋友数 $r$ 的实验

当 $n$ 固定为 $100$ , 初始朋友数 $r$ 从 $3$ 增加到 $30$, 每次增加 $3$ 时, $R$ 的变化如下图所示.

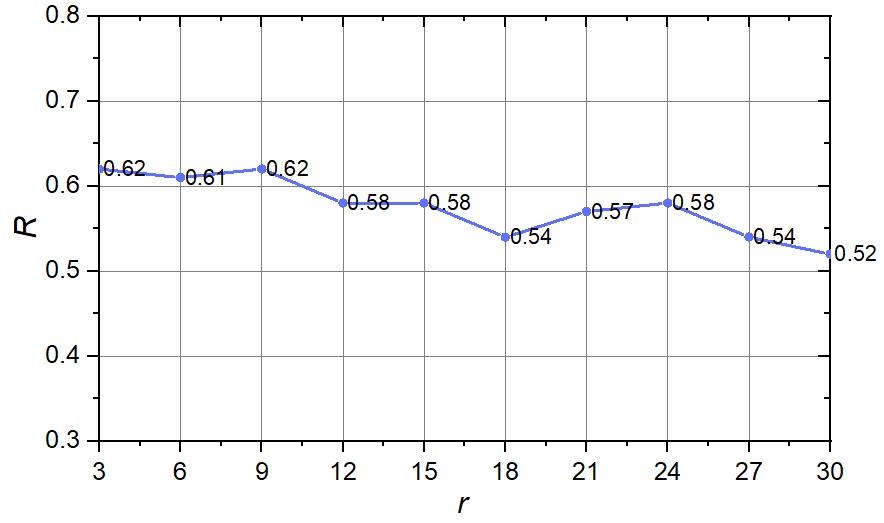
可以看到, 满足"友谊悖论"的人数占比整体上较稳定, 在 $[0.5, 0.7]$ 区间内, 且始终多于一半, 且整体上呈现出递减趋势.

在该网络模型中, 满足"友谊悖论"的人数占比较高于前一种模型, 是因为该网络的随机性更大, 并没有像上一种网络, 最开始就给大家分配好 $2\cdot r$ 个朋友, 再让整个网络进行演化, 而是只给每个人 $r$ 此交友机会, 因此朋友数量的方差较上一种网络会更大.

总结与思考

不论是从理论分析还是从模拟实验, 我们都会看到, "友谊悖论"的现象是存在的, 虽然整体上占比并不大 (大概在 $60\%$ 左右), 但也已经符合"大多数"人的定义. 因此, 感到自己的朋友似乎更受欢迎, 或有更会交友, 是很正常的一个现象. 因此与其为这种抽样偏差的结果所沮丧, 不如做好自己, 或者鼓起勇气, 多多主动结交有趣的人.

而在模拟实验中, 我所构造的社会网络也是最简单的两种形式, 一种是从确定的状态出发进行演化, 一种是从互不认识的状态开始随机交友, 这都是非常简单的模型. 实际上的社交网络模型会比这更复杂得多: 如我所采用的第二种模型, 不同性格的人也许交友意愿完全不同, 有的人愿意更多发出交友请求, 有的人则更内向与被动. 且交友往往也不是纯随机的过程: 如三元闭包原理告诉我们, 拥有共同朋友的人也往往会成为朋友. 因此, 本研究还有更多值得探索的方向, 可以尝试构造更复杂的社交网络. 目前的几个设想如下:

• 在随机型网络的基础上加入更多参数, 如每个人的主动交友数量的概率分布;

• 随机生成特定的网络后, 利用一系列增强手段添加或减少边 (甚至可以考虑图神经网络来完成增强), 而非只是随机删减边;

• 采用全新的网络生成思路, 如为每个节点构造各个属性值 (兴趣爱好, 居住地, 教育背景等), 使用聚类的方法生成网络.

因此, 友谊悖论的验证问题还有很多可以深入探讨.