马太效应与幂律分布

Posted on 2021-05-22 In 学术 Views:

简介

马太效应是在描述一种强者愈强, 弱者愈弱的两极分化现象. 该现象可以被归纳为: 任何个体, 群体或地区, 在某一个方面 (如金钱, 名誉, 地位等) 获得成功和进步, 就会产生一种积累优势, 就会有更多的机会取得更大的成功和进步.

反应这一模型的分布为幂律分布.

本文接下来会从数学角度对此问题进行分析, 对上述问题建立严格的数学模型, 进行一系列性质与定理的证明, 并给出该模型的模拟程序, 并研究其与幂律分布的吻合程度.

数学模型

考虑这样的建图算法:

共有 $n$ 个节点, 按照 $0,1,2,\cdots,n-1$ 的顺序依次创建.

首先创建节点 $0$.

当创建节点 $j(j\geq 1)$ 时, 以概率 $p$ 选择 (a) 执行, 以概率 $1-p$ 选择 (b) 执行:
(a) 在已有的 $j-1$ 个节点中均匀地, 随机地选择一个早先创建的网页 $i$, 建立一个从 $j$ 到 $i$ 的链接. 选中每一个节点的概率为 $1/(j-1)$.
(b) 按照与已有入度成比例的概率, 选择一个早先创建的网页 $i$，建立一个从 $j$ 到 $i$ 的链接. 选中每一个节点的概率与该节点的现有入度成正比.

该算法的代码实现如下 (使用 python 撰写):

M = np.zeros((n,n))
# 邻接矩阵，初始化全0
D = np.zeros(n)
# 每个节点的当前入度

def uniform_addedge(i):
	x = random.randint(0,i)
	M[i][x] = 1
	D[x] += 1

def addedge(i):
	if i == 0:
		return
	tmp_sum = 0
	for x in range(i):
		tmp_sum += D[x]
	weight_D = np.zeros(n)
	for x in range(i):
		weight_D[x] = float(D[x]/tmp_sum)
		weight_D[x] = weight_D[x] + weight_D[x-1]
	q = random.uniform(0, weight_D[i-1])
	for x in range(i):
		if q >= weight_D[x-1] and q <= weight_D[x]:
			M[i][x] = 1
			D[x] += 1
			return

for i in range(n):
	for j in range(k):
		q = random.uniform(0, 1)
		if q <= p:
			uniform_addedge(i)
		else:
			addedge(i)
            
max_D = int(np.max(D))
plt.hist(D,bins = max_D,label = 'Simulation Result')

理论推导

我们考虑节点入度的概率分布函数.

假设共有 $n$ 个节点, 初始选择时以 $p$ 的概率做均匀随机选择, 以 $q=1-p$ 的概率做加权随机选择, 每个节点的出度为 $k$.

仿照 $k=1$ 时的概率分布函数推导, 考虑 $k\neq 1$ 时的一般情况计算节点入度的概率分布函数:

对于时间 $t$, 节点 $j$ 的入度期望表示为 $X_j(t)$. 当 $t\leq j$ 时, 显然有 $X_j(t)=0$.

在时间 $t+1$ 时, 节点 $t+1$ 给 $j$ 一次链接的概率为:

$p_{t+1}(j) = p\cdot\frac{1}{t}+(1-p)\frac{X_j(t)}{t}.$

由于节点 $t+1$ 总共可以连 $k$ 条边, 因此节点 $t+1$ 给 $j$ 链接数量的期望为:

$\Delta X_{t+1}(j) = k\left(p\cdot\frac{1}{t}+(1-p)\frac{X_j(t)}{t}\right).$

因此 $X_j(t)$ 满足微分方程:

$\frac{ {\rm d}X_j(t)}{ {\rm d}t} =k\left(p\cdot\frac{1}{t}+(1-p)\frac{X_j(t)}{t}\right)$ $\Rightarrow \frac{1}{pk+qkX_j(t)}{\rm d}X_j(t)=\frac{1}{t}{\rm d}t$ $\Rightarrow X_j(t)=\frac{1}{qk}\left(\frac{pk}{j^{qk}}\cdot t^{qk}-pk\right)$ $\Rightarrow X_j(t)=\frac{p}{q}\left(\left(\frac{t}{j}\right)^{qk}-1\right).$

考虑 $t$ 时刻入度至少为 $x$ 的节点个数:

$X_j(t)=\frac{p}{q}\left(\left(\frac{t}{j}\right)^{qk}-1\right)\geq x$ $\Rightarrow j\leq t\cdot\left(\frac{q}{p}\cdot x+1\right)^{-\frac{1}{qk}}$ $\Rightarrow P(x)=p(X\leq x)=1- t\cdot\left(\frac{q}{p}\cdot x+1\right)^{-\frac{1}{qk}}$

这是满足幂律分布的.

现考虑其离散化的情况. 记 $N(x)$ 为入度为 $x$ 的节点的数量. 在绘制真正的幂律分布函数图像时, 我们直接令:

$N(x)=\int_{x}^{x+1} p(x){\rm d}x = P(x+1)-P(x).$

其中 $P(x)$ 是上面已经计算出的 $\rm CDF$, $p(x)=P'(x)$ 是 $\rm PDF$.

这一部分的代码如下:

1
2
3

x=np.linspace(0,np.max(D),np.max(D))
power_func = ((1-((1-p)/p*(x+1)+1)**(-1/((1-p)*k)))*n-(1-((1-p)/p*x+1)**(-1/((1-p)*k)))*n)
plt.plot(x, power_func,label = 'Power Law Result')

实验结果

使用控制变量法进行实验, $n,p,k$的默认值分别为 $500, 0.6, 3$.

对于不同的 $n,p,k$, 模拟的结果与幂律分布的图像如下:

改变 $n$ 的实验

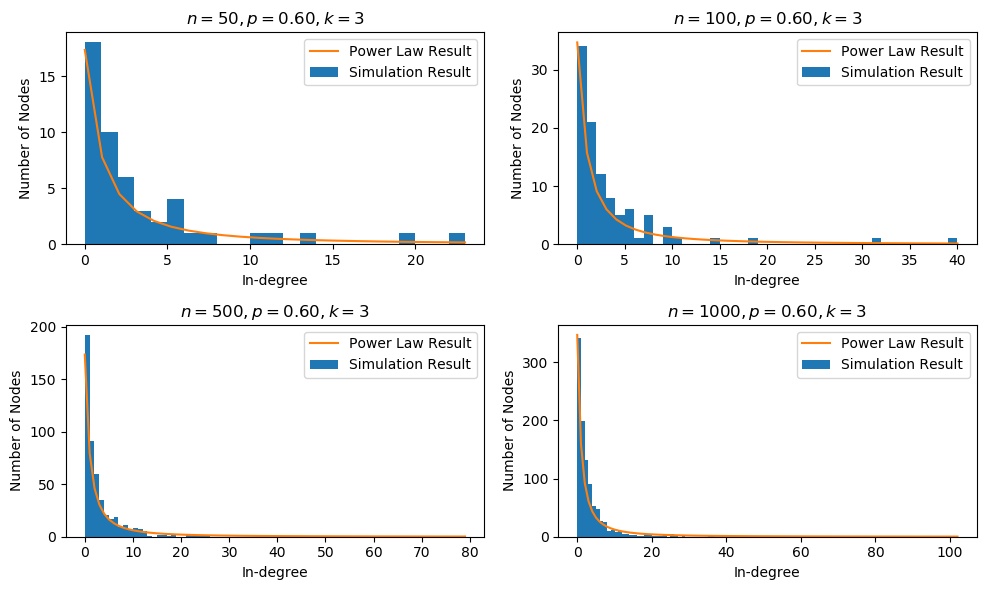
可以看到, $n$ 越大, 实验结果越接近真实的幂律分布.

改变 $p$ 的实验

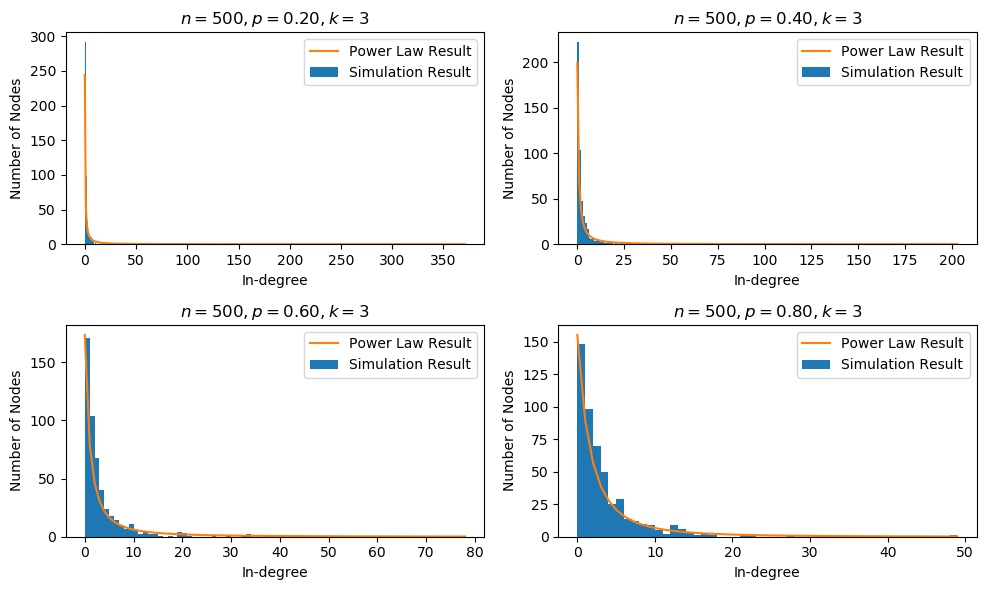
可以看到, 结果与幂律分布始终很吻合, 且 $p$ 越小, 分布越极端.

改变 $k$ 的实验

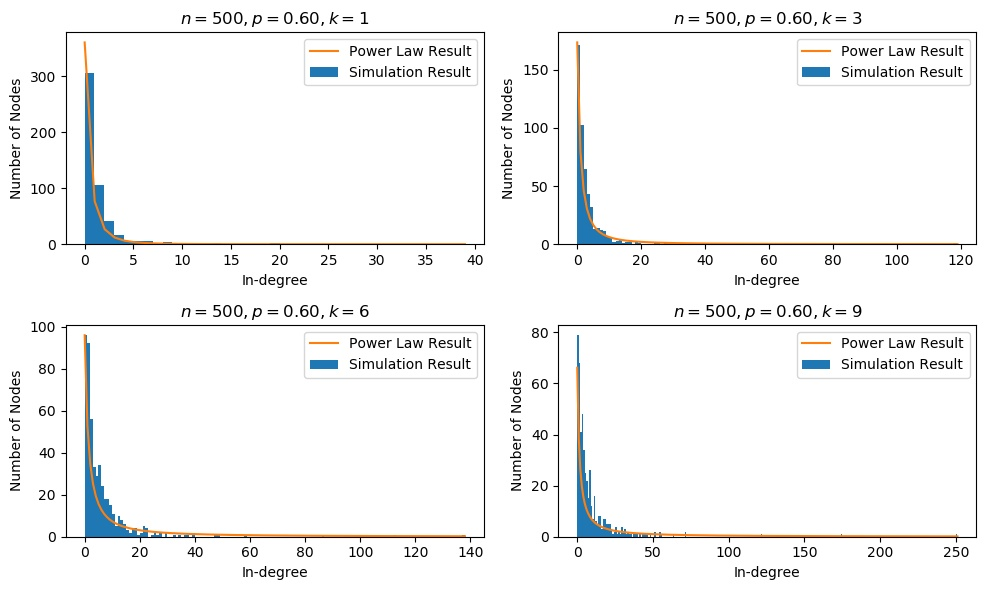
可以看到, 结果与幂律分布始终很吻合.